はじめに
建設や機械設計などの分野を支える材料力学において、構造物が外部からの力を受けた際、その内部でどのような状態になっているかを正確に把握することは極めて重要です。特に、物体が破壊に至る原因となる「応力(単位面積あたりの内力)」の変化を理解する必要があります。
今回解説する「モールの応力円」は、この複雑な応力成分の変化の様子を、誰にでもわかるように視覚化した非常に便利な図です。
この図は、ドイツの応用力学者モールによって考案されました。モールの応力円を用いることで、任意の断面で発生する垂直応力 (σ) とせん断応力 (τ) の関係を視覚的に捉え、構造物にとって最も危険な最大応力や最小応力を瞬時に読み取ることが可能になります。
この記事では、まず応力の基本となる仮想断面の考え方から、応力円が示す破壊現象との関連性、そして応力円の具体的な作成手順までをわかりやすく解説します。
本文
1. 応力の基本:仮想断面と内力
物体が左右から同じ力で引っ張られているなど、外力を受けながら静止して釣り合っている状態を考えます。このとき、物体内部には釣り合いを保つ力が働いています。これを内力と呼びます。
内力を知るために便利なのが、仮想断面という考え方です。
💡 仮想断面とは? 実際に物体を切ることはできませんが、頭の中で仮想的に切断した断面を考えます。これにより、力学的な釣り合いを維持したまま、内部に働く内力を把握することができます。
この仮想断面をどのように切断しても、内部に働く内力 (BやP) の大きさ自体は変わりません。
しかし、応力は「内力 / 断面積」で定義されるため、仮想断面の切り方(傾き)によって断面積が変化すると、応力も変化することになります。例えば、丸棒を軸に垂直に切った断面(断面積A)に対し、角度θだけ傾けて切った断面の断面積は cosθ / Aと表されます。
2. 応力の分解と斜め断面の重要性
応力は、断面の切り方によって、常に二つの成分に分解して考える必要があります。
| 応力の成分 | 記号 | 説明 |
|---|---|---|
| 垂直応力 | σ | 断面に垂直に働く応力成分。微小な領域を垂直に引っ張る力。 |
| せん断応力 | τ | 断面に沿って(水平に)働く応力成分。 |
ここで重要なポイントは、丸棒を単純に引っ張るような状態であっても、斜めの仮想断面を考えると、その面には垂直応力 (σ) だけでなく、せん断応力 (τ) が必ず発生するということです。
🟦 角度による応力変化の例
仮想断面の傾き(角度θ)が変わると、σとτの大きさも変化します。
| 傾斜の角度 (θ) | 垂直応力 (σ) | せん断応力 (τ) |
|---|---|---|
| 0度(軸に垂直な面) | 最大となる。 | ゼロとなる。 |
| 45度 | σとτが同じ大きさになる。 | 最大となる。 |
| 90度 | ゼロとなる。 | ゼロとなる。 |
📌 破壊現象と45度の関係
「壊れないものを作る」ためには、斜めの仮想断面にかかる応力(σとτ)を考慮することが不可欠です。
例えば、強い地震の後に柱や壁に斜めのひび割れが入ることがあります。これはせん断破壊と呼ばれ、せん断応力 (τ) によって構造物が壊れた結果です。
コンクリートは圧縮力には強い性質を持ちますが、引張力が作用する状態では、せん断応力が最大となる45度の面で破壊が進む傾向があります。斜めのひび割れは、まさにこの45度面でせん断応力が最大になったことの証拠なのです。
3. モールの応力円の仕組みと特徴
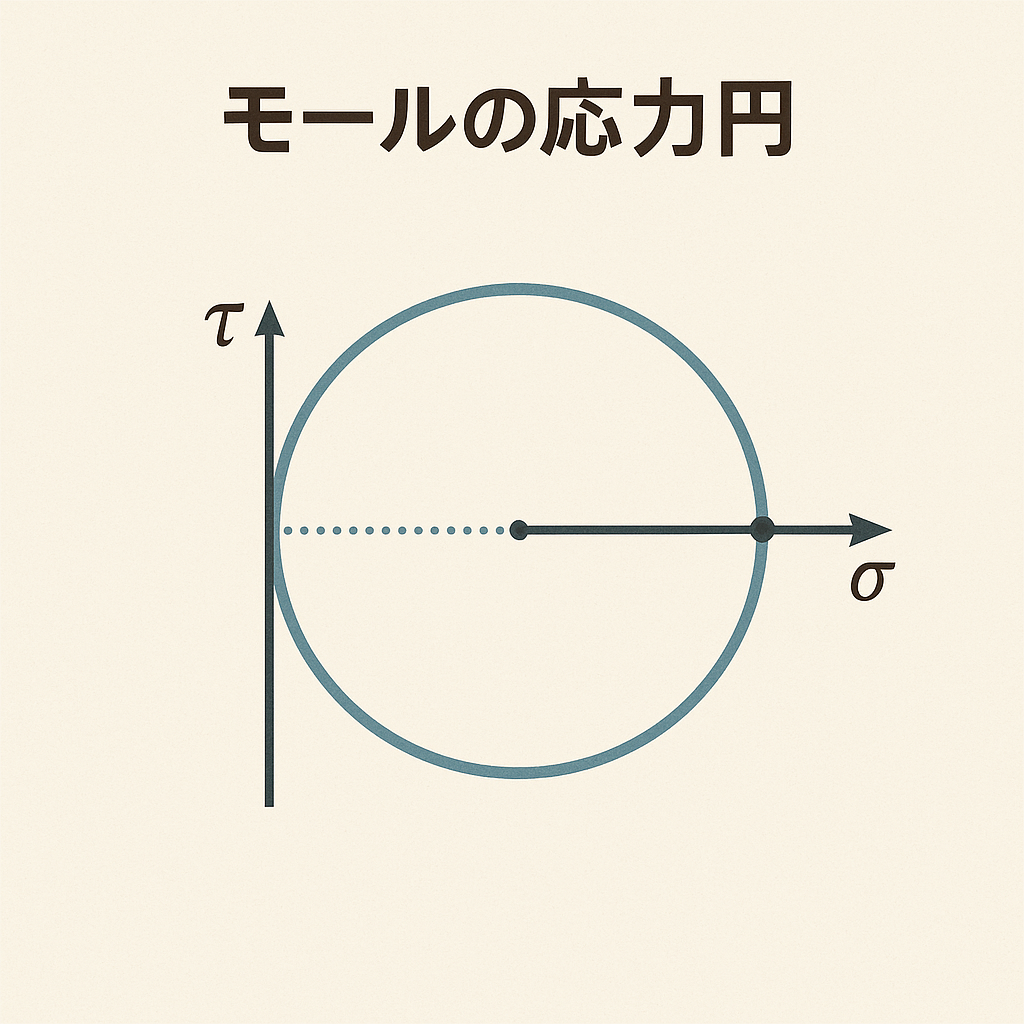
モールの応力円は、仮想断面の角度 (θ) を変化させた場合の垂直応力 (σ) とせん断応力 (τ) の変化の様子をグラフに示したものです。
🟦 円が描かれる仕組み
数式に基づき、角度θ を-90度から90度、あるいは0度から180度まで変化させながら、計算された垂直応力 (σ) を横軸に、せん断応力 (τ) を縦軸にとってプロットすると、その軌跡は驚くほどきれいな円となります。
この円は、水平軸上(σ軸)に中心を持つことがわかっています。
🟦 モール応力円の主要な特徴
- 周期性: 仮想断面の角度θが180度変化するごとに、応力円は一周します。
- 最大応力点: 垂直応力(σ) が最大値または最小値となる点では、せん断応力 (τ) の値は必ずゼロになります。
4. モールの応力円の作成手順と活用
モールの応力円は、与えられた応力状態(基準面)から、発生しうる最大応力値を導き出すために活用されます。
🟦 応力円の簡単な作図手順
複雑な計算をせずに応力円を描くための手順は以下の通りです。
- 基準面をプロット: 評価の基準とする面(基準面)の垂直応力 (σ) とせん断応力 (τ) の組み合わせをグラフにプロットします。
- 90度面をプロット: その基準面と直交する面(90度の面)の σとτ の組み合わせをグラフにプロットします。
- 円を描く: プロットしたこの2点(基準面と90度面)を直径の両端とする円を描けば、モールの応力円が完成します。
この手順により、任意の応力状態(例:2方向に応力がかかるケースや、垂直応力とせん断応力が同時にかかるケースなど)に対しても、モールの応力円を作成できます。
🟦 モール応力円の視覚的活用
応力円が完成すると、その円周上にある点が、その応力状態において発生しうるすべての (σ, τ) の組み合わせを示します。
これにより、以下の重要な応力値を視覚的に把握することができます。
- 最大垂直応力 (σ{max}):円の最も右側の点
- 最小垂直応力 (σ{min}):円の最も左側の点
- 最大せん断応力 (τ{max}):円の最上部または最下部の点
これらの最大・最小値を把握することは、構造物の安全性を評価する上で非常に役立ちます。
まとめ
モールの応力円は、材料力学における応力解析の基本であり、最も強力なツールの1つです。
🟦 モールの応力円の要点
- 定義: 仮想断面の角度変化に伴う垂直応力 (σ) とせん断応力 (τ) の組み合わせを、σを横軸、τを縦軸とするグラフ上で描いた円形の軌跡のこと。
- 重要性: 応力は仮想断面の選択(傾き)によって変化するという核心概念に基づき、その変化をすべて視覚的に表現する。
- 利点: 応力円の図を用いることで、複雑な応力計算をせずに、構造物の最大垂直応力や最大せん断応力といった最も危険な状態を瞬時に判断できる。
- 作成: 基準面とそれと直交する面(90度の面)の応力値をプロットし、これらを直径とする円を描くことで完成する。
モールの応力円を理解することで、単なる引っ張りや圧縮に見える現象の裏に潜むせん断破壊(斜め45度の破壊)といったリスクを正確に評価し、より安全で丈夫な構造物や部品の設計が可能となるのです。

コメント